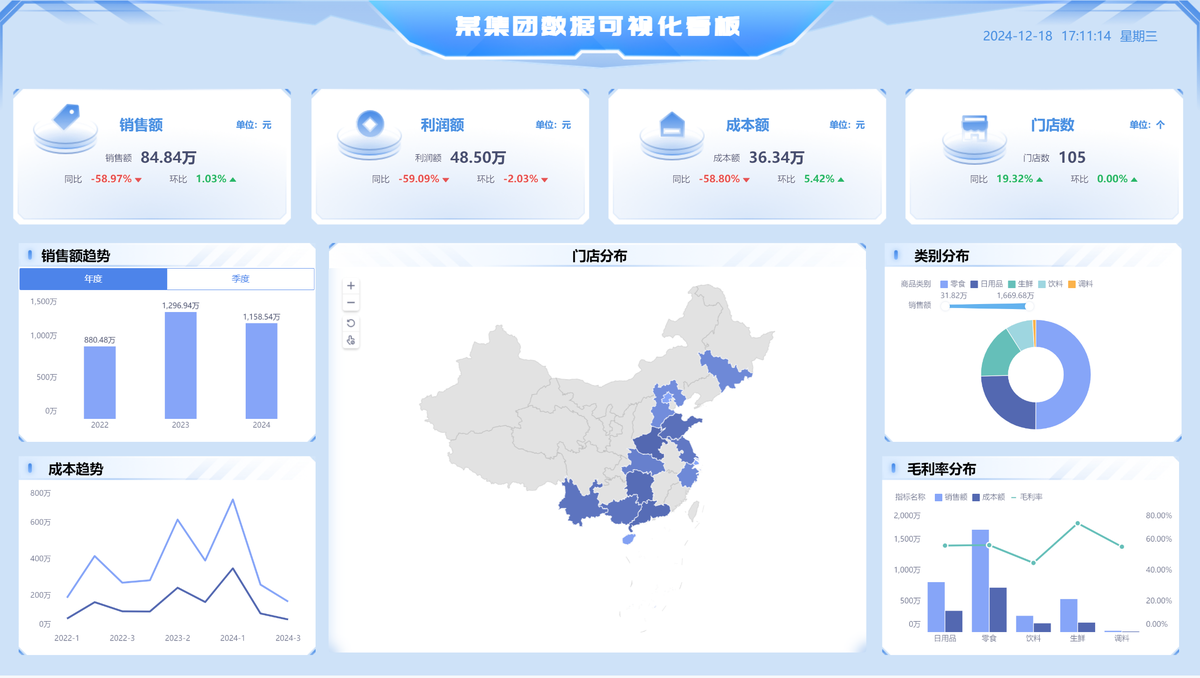
小白友好！一文讲清楚统计学里的t检验、方差分析等8大数据分析方法！ | 帆软九数云
数据分析方法，其实就是数据分析界的SOP；帮你把“问题 → 分析 → 结论”的路径标准化，这样就让任何分析师面对同样的问题都能用相似的方法得出可靠结果，既提高效率，也保证质量。
那么数据分析师最经典的8大分析方法是什么？在什么场景下用？今天一篇文给你讲清楚！
1、t检验
用来比较两组数据均值差异的方法，常用于样本数量较少（通常< 30）、且数据大致符合正态分布的场景。
t检验分为单样本t检验、独立样本t检验、配对t检验
- 单样本 t 检验：比较一组数据均值和一个已知数字之间是否有显著差异（比如月均销售额是否达到xx）
- 独立样本t检验：比较两组独立样本的均值差异（如做法A与做法B的效果对比）。
- 配对样本t检验：比较同一组数据在不同条件下的均值差异（如治疗前后的效果对比）。
示例：
研究两组志愿者体重变化，输出结果如下
p：原假设成立时，出现当前或更极端样本结果的概率
t：综合数据均值差、样本标准差、样本量等计算出的统计量
解读：
1、先看p:p=0.525<0.05；说明差异不显著
2、再看t：t=-0.642；说明x2组体重略高
结论：
两组志愿者体重变化没有显著差异
2、方差分析
用于比较三组及以上连续数据的均值差异；
方差检验分为单因素方差分析和多因素方差分析
- 单因素方差分析：只有一个分组变量
- 多因素方差分析：两个及以上分组变量
示例：
研究3个班级学生成绩的差异，输出结果如下：
F 值：组间均方与组内均方的比值
p 值：是在原假设（多组数据无差异）成立时，出现当前或更极端 F 值的概率
解读：
1、先看p 值，若\(p < 0.05\)（如这里\(p = 0.043\)），说明多组数据（3 个班级成绩）间存在显著差异；
2、再看各组平均值，对比可知 3 班成绩平均值（89.444）明显低于 1 班（113.333）和 2 班（127.222），能进一步明确具体差异情况。
结论：
3 班成绩平均值明显低于 1 班和 2 班。
3、卡方检验
卡方检验用于分析定类数据与定类数据之间的差异情况，包含5种类型：
- 独立性卡方检验：判断两个分类变量是否相关或独立。
- 配对卡方检验：判断同一组对象的二分类变量前后变化是否显著。
- 卡方拟合优度检验：判断一个分类变量的实际分布是否符合理论分布。
- 分层卡方检验：在分层或分组数据下检验两个变量的独立性，同时控制混杂因素。
- Fisher精确检验：样本量小或某些格子频数很低时，用于判断两个分类变量是否相关，比卡方检验更精确。
示例：
研究不同班级（重点班 & 普通班）学习成绩（优秀、及格、不及格）的差异，输出结果如下：
χ²：卡方检验中衡量实际观测与理论期望差异程度的统计量
p值：是判断这种差异是否具统计学显著性的概率指标
解读：
1、先看p 值，p = 0.000 < 0.01，说明不同班级（重点班和普通班）的成绩存在极显著差异；
2、再看括号内百分比，普通班及格人数占比最高（50%），重点班优秀人数占比最高（64.516%）且不及格占比最少（16.129%）。
结论：
不同班级的学习成绩呈现出极显著差异，重点班优秀率更高、不及格率更低，普通班及格率更高。
4、相关分析
用于两个变量是否有关系，以及关系的紧密程度
- 当数据满足正态分布时用 Pearson 相关分析
- 当不满足正态分布用 Spearman 相关系数。
示例：
分析体重与双肾总体积之间是否有相关关系，输出结果如下：
相关系数：衡量变量间相关关系紧密程度的统计量，相关性越强，绝对值越接近1
星号：其实就是p值的标识，1个代表p<0.05，2个代表p<0.01
解读步骤：
1、先看是否有 * 号，有2个，说明显著相关；
2、再看相关系数大小，相关系数越大则相关性越强；
结论：
本案例中相关系数为 0.875 且带有 **，说明体重与双肾总体积之间存在显著正相关关系。
5、 多元线性回归
研究一个因变量受多个自变量影响的程度，例如销量受价格、广告费、活动类型影响。
示例：
研究多个变量（教育程度、初始工资、工作经验、年龄等）对工资的影响关系，输出结果如下：
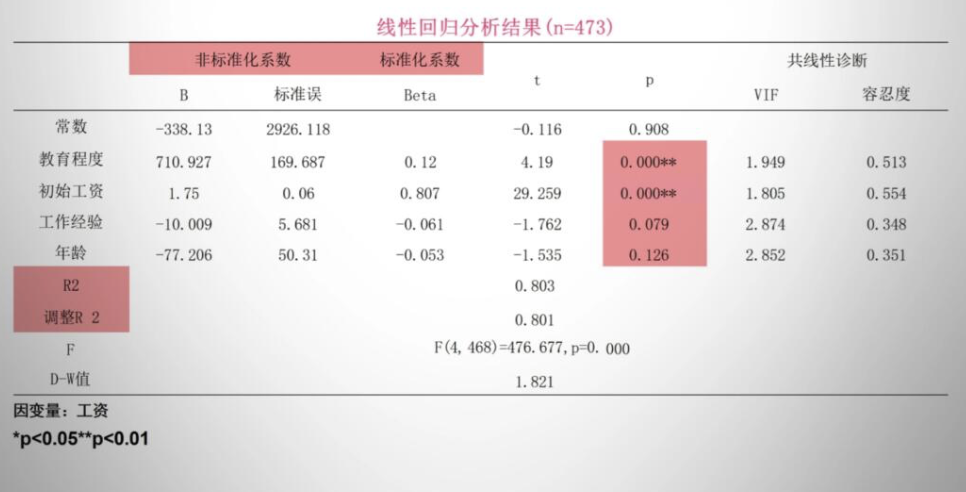
t：是检验回归系数是否显著的统计量，用于判断自变量对因变量的影响是否 “靠谱”。
p：是 t 检验对应的概率值，若p < 0.05或p < 0.0，说明自变量对因变量的影响显著。
VIF（方差膨胀因子）：用于衡量自变量间多重共线性的程度，VIF 越大，共线性越严重。
容忍度：是 VIF 的倒数，同样用于判断多重共线性，容忍度越小，共线性越严重。
解读：
1、先看是否有 * 号，若有，说明该变量对工资影响显著，上述可以看到初始工资、教育程度影响很强
2、再看回归系数（B 或 Beta），系数正负表示影响方向，绝对值大小反映影响程度
3、同时可参考R²=0.803，了解模型对 Y 变异的解释程度；
结论：
教育程度、初始工资对工资有极显著的正向影响，工作经验对工资有边际显著的负向影响，年龄对工资影响不显著，模型能解释工资 80.3% 的变异，拟合效果较好。
6、主成分分析（PCA）
是一种降维的方法，把数据中有相关性的指标归到一类
比如你有100个学生的成绩数据：语文、数学、英语、物理、化学、生物。各科成绩互相关联（数学好，物理通常也好）；于是可以把6门成绩压缩成2个核心指标：
- 核心指标1 → 理科能力；
- 核心指标2 → 文科能力
这样你只看两个指标，就能大致了解每个学生的学业水平。
7、因子分析
把很多相关的观测指标归纳成少数几个潜在“因子”，用这些因子来解释数据背后的结构或模式。
同样用上述主成分分析的例子，你有100个学生成绩，你在里面发现
- 语文、英语、历史往往一起好 → 可能有一个“文科能力因子”
- 数学、物理、化学、生物往往一起好 → 可能有一个“理科能力因子”
这样就可以多个相关指标背后的共同因素提取出来，抓住数据的核心结构，让复杂数据变得更容易理解。
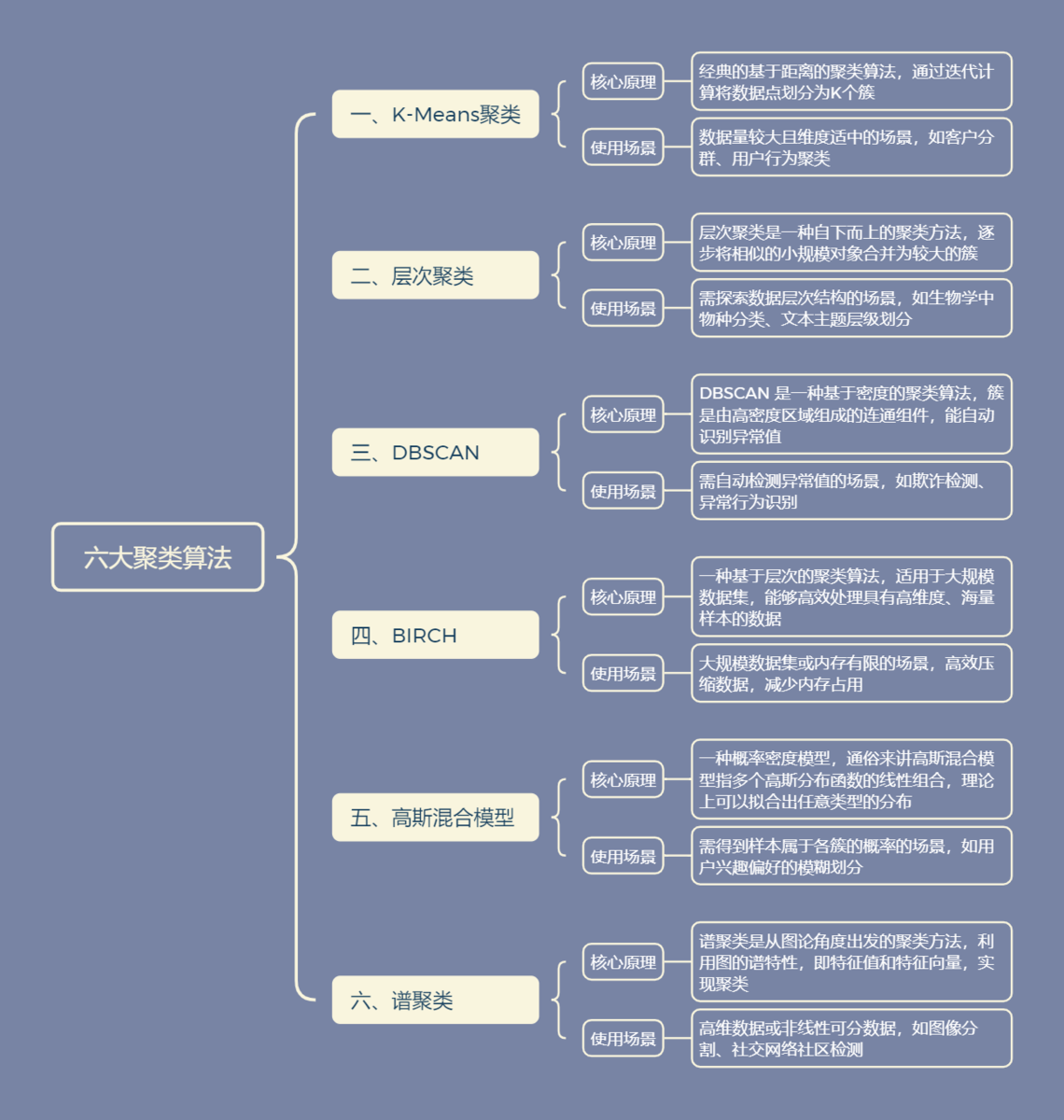
8、聚类分析
把没有标签的数据分群，常用于客户分层、产品分组、市场细分。常见的有6种聚类分析方法
- K-Means适合球形簇、快速分群；
- 层次聚类可探索数据层次结构，适合小数据量；
- DBSCAN能识别任意形状簇并检测异常值；
- BIRCH适合大规模数据，内存高效；
- 高斯混合模型（GMM）提供样本属于各簇的概率，处理簇重叠；
- 谱聚类适应高维、非线性数据，灵活处理复杂簇形状。
学会这8大分析方法，建立自己的数据分析图谱，以后任何杂乱的数据都难不倒你啦！
热门产品推荐
本文将介绍如何利用表格生成柱状图提升数据分析效果，帮助读者更好地理解和呈现数据。
九数云 | | 2023-11-10
数据分析工作是目前运营商务工作的重点，今天小九就来为大家介绍数据分析工作专业术语有哪些~
九数云 | | 2023-10-20
指数加权移动平均（EWMA，或EMA）作为一种常用的平滑方法，通过赋予近期数据更高的权重，使得分析结果能更快速地响应变化，并能有效地应用于各个领域。
九数云 | | 2025-09-28
线上图表，作为一种直观的数据呈现方式，在信息时代扮演着越来越重要的角色。它能够将复杂的数据转化为易于理解的视觉形式，帮助人们快速捕捉数据背后的规律和趋势。无论是商业分析、学术研究还是日常汇报，精美的线上图表都能有效提升沟通效率和决策质量。现在，越来越多的免费线上图表工具涌现，降低了数据可视化的门槛，让每个人都能轻松创建专业级的图表。
九数云 | | 2025-12-24
在商业经营领域，现在市面上有什么比较好用的大屏软件呢？
九数云 | | 2024-05-20
报表布局，作为数据报表设计的基础，直接影响着报表的可读性、易用性和最终的决策效果。
Jamie | | 2025-06-18
