1天1个数据分析模型:什么是回归分析? | 帆软九数云

很多人第一次听到“回归分析”这个词,都觉得离自己很远。但其实我们生活中经常用到这个模型:你每天看到的广告投放回报、天气与饮料销量的关系、房价预测、销售预算模型……背后几乎都在用回归分析。
这篇内容,我们就用一个通俗的例子,带你从0开始搞懂:
- 什么是回归分析
- 它能干什么
- 常见的7种回归模型
- 如何做出一个能落地的回归分析模型
一、什么是回归分析?
回归来自英文单词 regression 最早是统计学家 Francis Galton;
在研究“父母与孩子的身高关系”时, 他发现: 高个子的父母,孩子往往没那么高;矮个子的父母,孩子也不会特别矮。
换句话说,孩子的身高总是“向平均值靠近”一点。 他把这个规律称为 Regression to the mean——“向平均值回归”。
后来统计学家们用类似的数学原理,去研究“一个变量随着另一个变量变化的趋势关系”;
于是,“回归分析(Regression Analysis)”这个名字就沿用了下来。
二、回归模型能干嘛?
回归分析是数据分析里最常用、最实用的预测模型之一。能帮你回答:
- “广告花的钱,能不能带来更多销量?”
- “客单价高的客户,是不是复购率也高?”
- “温度对饮料销量的影响大不大?”
- “门店面积越大,营业额是不是越高?”
它的本质就是一句话:用历史数据去量化“一个东西”对“另一个东西”的影响关系。更深入一层,回归分析能干3件事:验证假设、预测结果、评估影响。
1、验证假设
在现实生活和工作中,我们会把很多因素关联起来,比如:
- 广告投多一点肯定能带来销量
- 天气热,饮料就卖得好
- 新用户注册越多,收入肯定越高
等等,回归分析可以用数据帮你把这些假设做验证。
2. 预测结果
预测有两种情况:
- 连续型预测。
比如:预测销售额是多少,预测下个月来客数是多少,预测今年利润能不能破千万。
这类问题的答案通常是一个具体的数字,是连续变化的结果。
举个例子,你可能建立一个模型,用广告投放金额、门店数量、平均价格等因素去预测“销售额”。 最后跑出来的结果可能是:“根据历史关系,本月预计销售额在 3550 万左右。” 这类模型最典型的就是线性回归、多元回归,都是预测一个具体数值。
- 分类预测
比如:预测客户会不会流失?用户会不会接电话?一款新产品上市后能不能成为爆品?
这些问题的答案,不是一个数字,而是一类结果。 比如“会 / 不会”、“高 / 中 / 低”、“A 级 / B 级 / C 级”。 这时候我们就会用到“逻辑回归(Logistic Regression)”这类方法。
3、评估影响
第二个作用,是帮你判断:到底谁的影响最大——回归分析能量化每个因素对结果的影响程度。引入很多个变量,看哪个变量影响最大也就成为可能。
举个例子。 你想提升门店业绩,但你不确定该先优化哪个方面。 于是你收集了每家门店的各种数据:
- 员工数量
- 门店面积
- 促销频率
- 顾客满意度
- 周边竞争强度
然后计算每个变量的回归系数,就可以发现哪些是关键影响因素,哪些没有什么影响;这时候你就知道该往哪使劲了。
三、常见的7种回归模型
回归分析有一整个家族,不同的回归方法,针对不同问题。
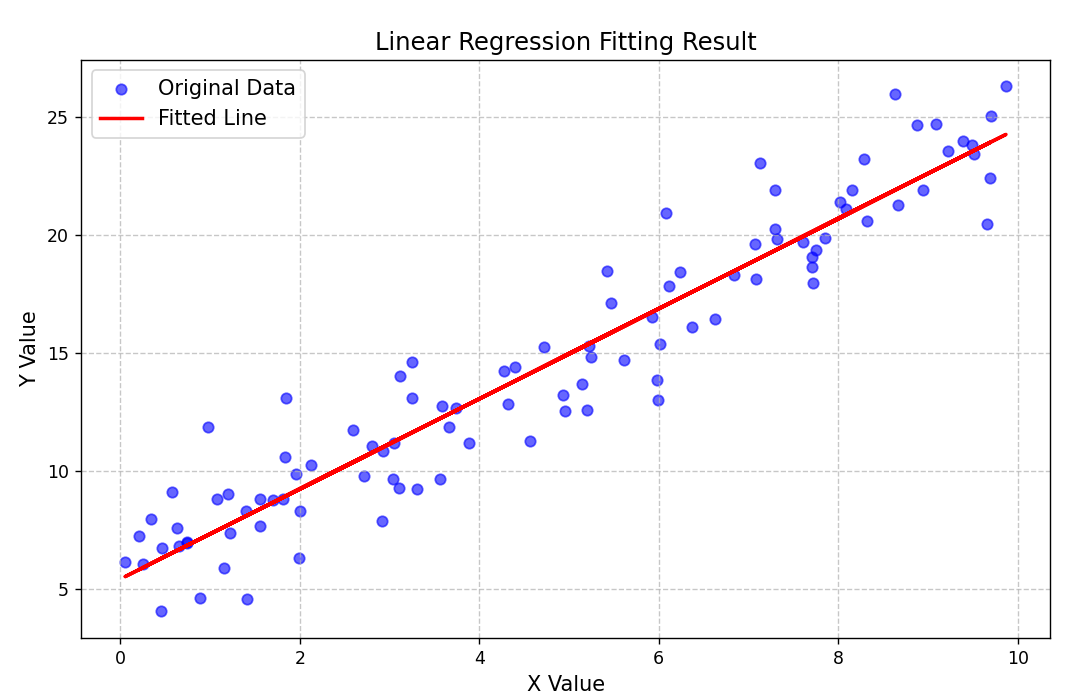
1. 线性回归
线性回归假设因变量与自变量呈线性关系,用直线描述。
适用于
- 因变量是连续变量,如收入、温度、销量
- 自变量与因变量的关系近似直线,可通过散点图判断
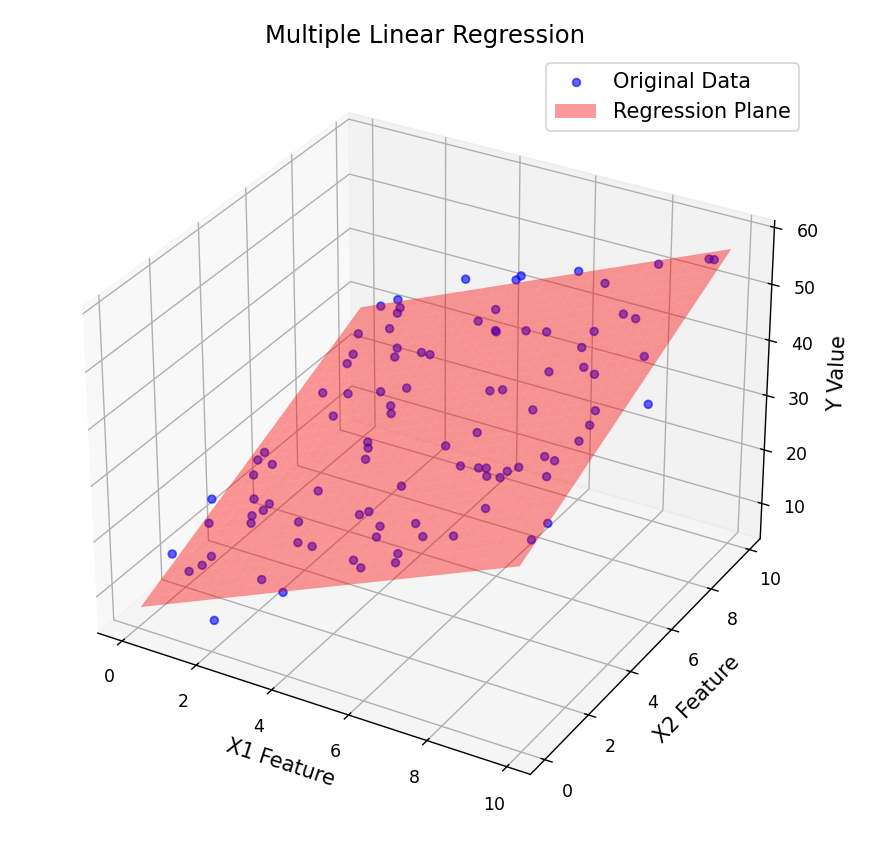
2. 多元线性回归
多元线性回归在简单线性回归的基础上,纳入多个自变量,分析它们对因变量的共同影响。
适用场景:
- 因变量受多个因素影响,现实中绝大多数问题都是如此
- 多个自变量与因变量均呈线性关系。
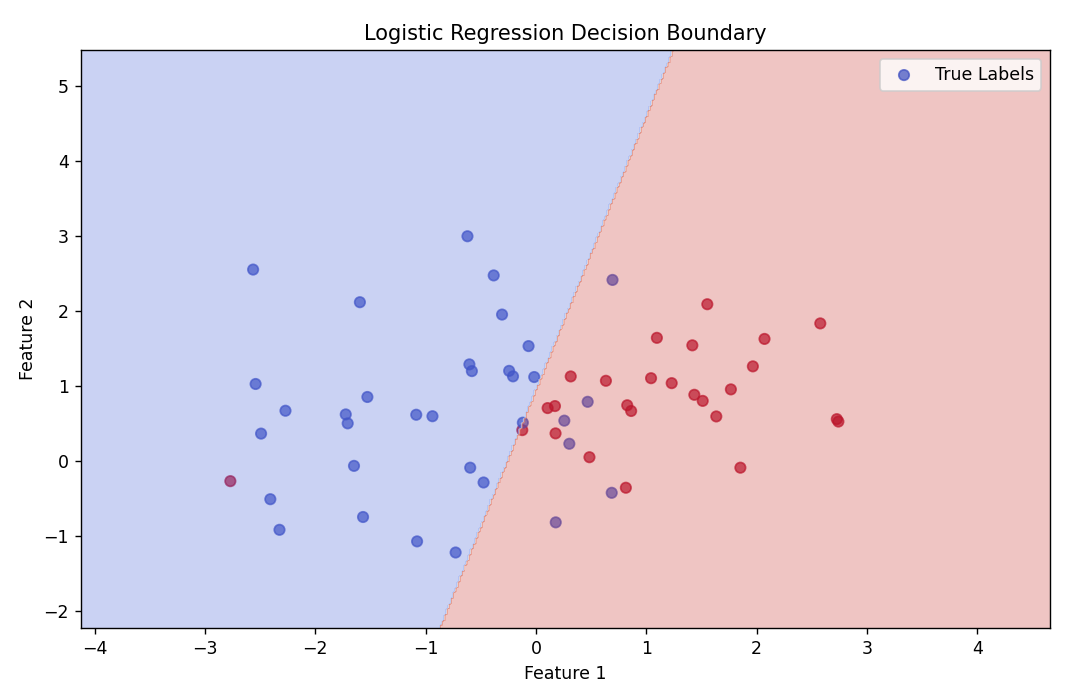
3. 逻辑回归
逻辑回归的因变量是二分类变量,如 是/否、发生/不发生,通过公式将结果映射到 0-1 之间。
适用于
- 因变量是分类变量,且只有两个结果,如用户是否点击广告、患者是否患病;
- 想预测某事件发生的概率
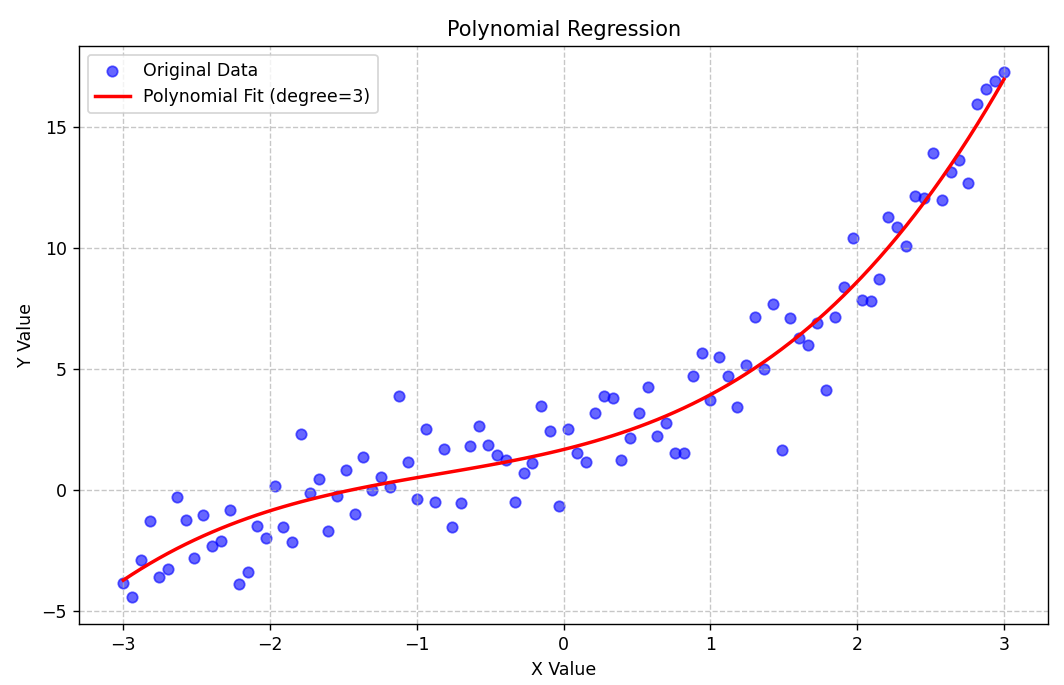
4. 多项式回归
多项式回归是当自变量与因变量的关系是曲线,如二次曲线、三次曲时,用多项式拟合。
适用于:
- 变量间关系不是直线,比如 年龄与收入:年轻时收入随年龄增长快,中年后增长放缓甚至下降
- 散点图呈现明显的曲线趋势
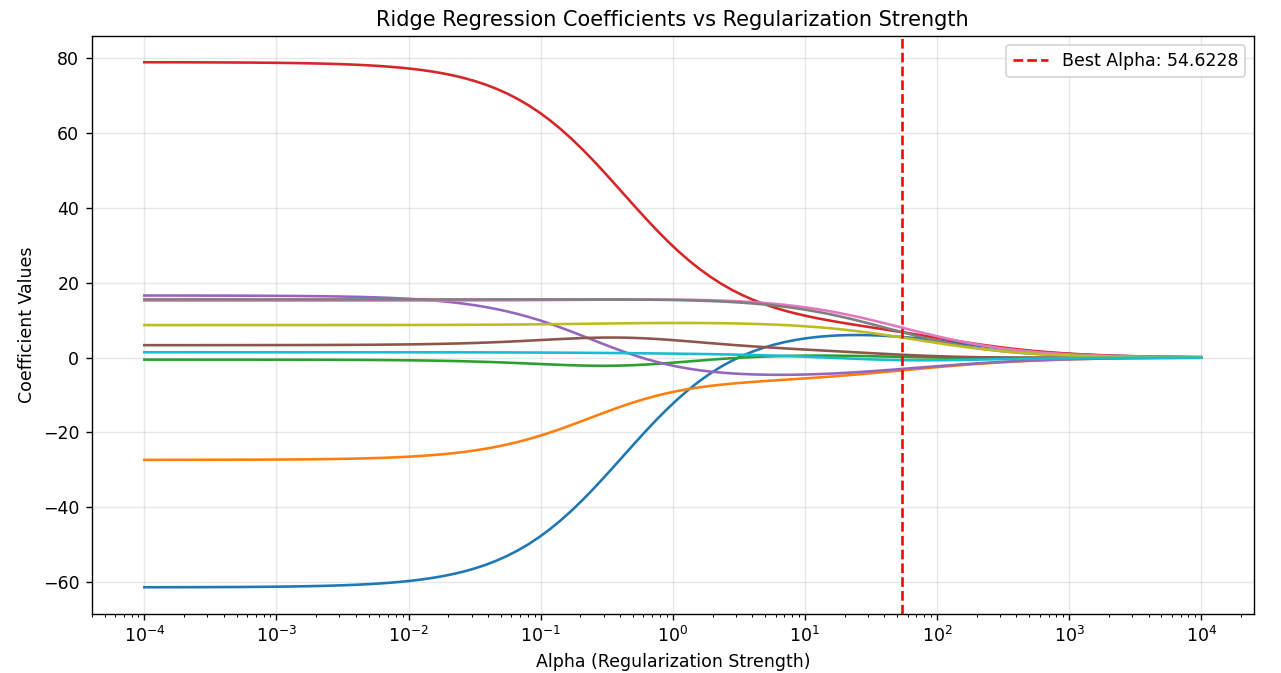
5. 岭回归
岭回归是当自变量之间高度相关时,通过正则化避免结果失真。
适用场景:
- 自变量数量多,且存在强相关性
- 线性回归结果不稳定
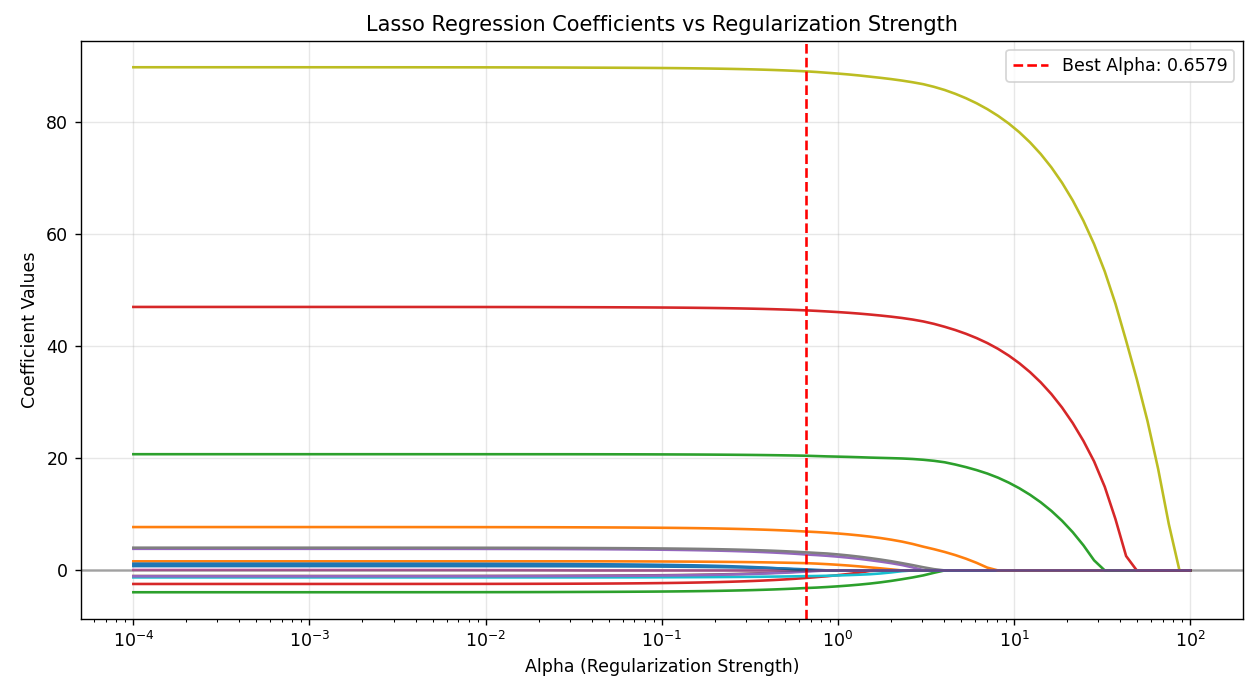
6. LASSO 回归
LASSO 回归不仅能解决多重共线性,还能通过正则化压缩部分自变量的系数为 0,自动实现变量筛选。
适用场景:
- 自变量数量极多,如基因数据、用户行为特征,想找出真正有影响的因素
- 希望模型更简洁,只保留关键变量
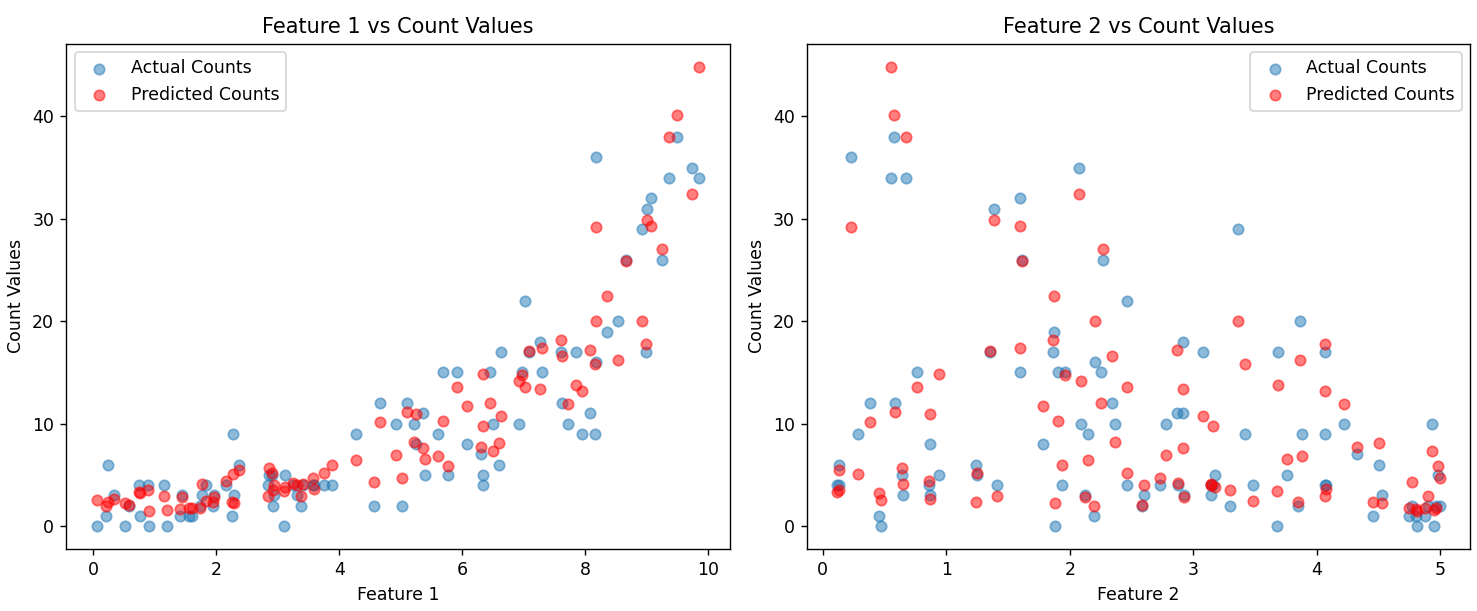
7. 泊松回归
泊松回归的因变量是计数变量,如 一定时间内的发生次数,且数值是非负整数。
适用场景:
- 因变量是事件发生的次数,如 每月交通事故数、患者每天咳嗽次数
- 数据呈现右偏分布
四、如何进行回归分析?
这里拿一个最简单的线性回归预测的例子俩给大家说明白:
例子:
某公司在新品上市前,会提前宣传并开放预约。虽然最终购买的不一定都是预约用户,但如果能根据预约人数预测销量,就能提前预判市场热度,合理安排备货量。
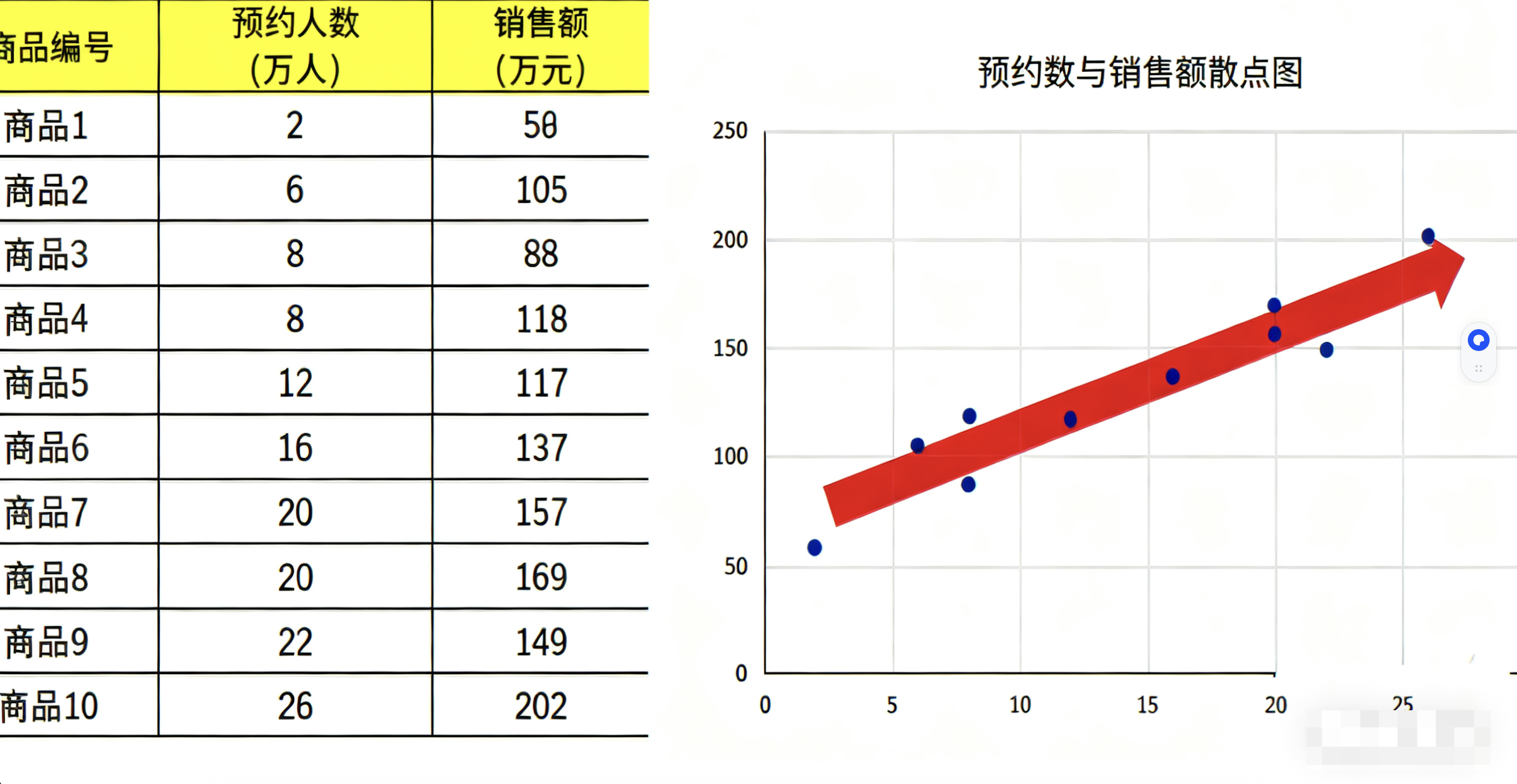
拿到问题后,一步步来:
第一步:确认是否是预测问题
先搞清楚你想解决的问题类型。这里我们要预测“销售额”,它是一个连续型变量(可以取任意数值),所以属于典型的预测类问题。
第二步:确认因变量,自变量
这一步是回归分析的核心:
- 因变量(Y):你要预测的目标,也就是销售额。
- 自变量(X):可能影响目标的因素,这里是预约人数。
接下来要判断——这两个指标之间有没有关系?关系是线性的还是非线性的?
最简单的办法就是:画散点图!
如果点的分布大致在一条直线附近,那说明存在线性关系,可以直接用线性回归建模。 假设我们画出来的图像呈现明显的上升趋势,那就可以继续往下做了。
第三步:收集数据
这个步骤通常是最费时间的,但题目已经帮我们准备好了数据集。 所以直接进入下一步。
第四步:进行计算
做线性回归最方便的工具是 Excel: 在菜单栏里找到【数据分析】 → 选择【回归】,输入因变量和自变量区域,就能自动生成一整套结果表。
如果数据量较大或需要频繁建模,可以直接在 BI 工具中封装回归分析模型,比如在九数云、Power BI、Tableau 等平台,都可以实现自动化建模与预测。
九数云官网,免费试用:https://www.jiushuyun.com/
模型解读
很多人到这步就懵了——一堆表格,一堆系数,看不懂。其实可以抓三件最关键的事来看:
- 模型准不准 → 看 R²(决定系数)
- 整体是否有效 → 看 F检验 的结果
- 每个变量是否显著 → 看 t检验 和显著性(P值)
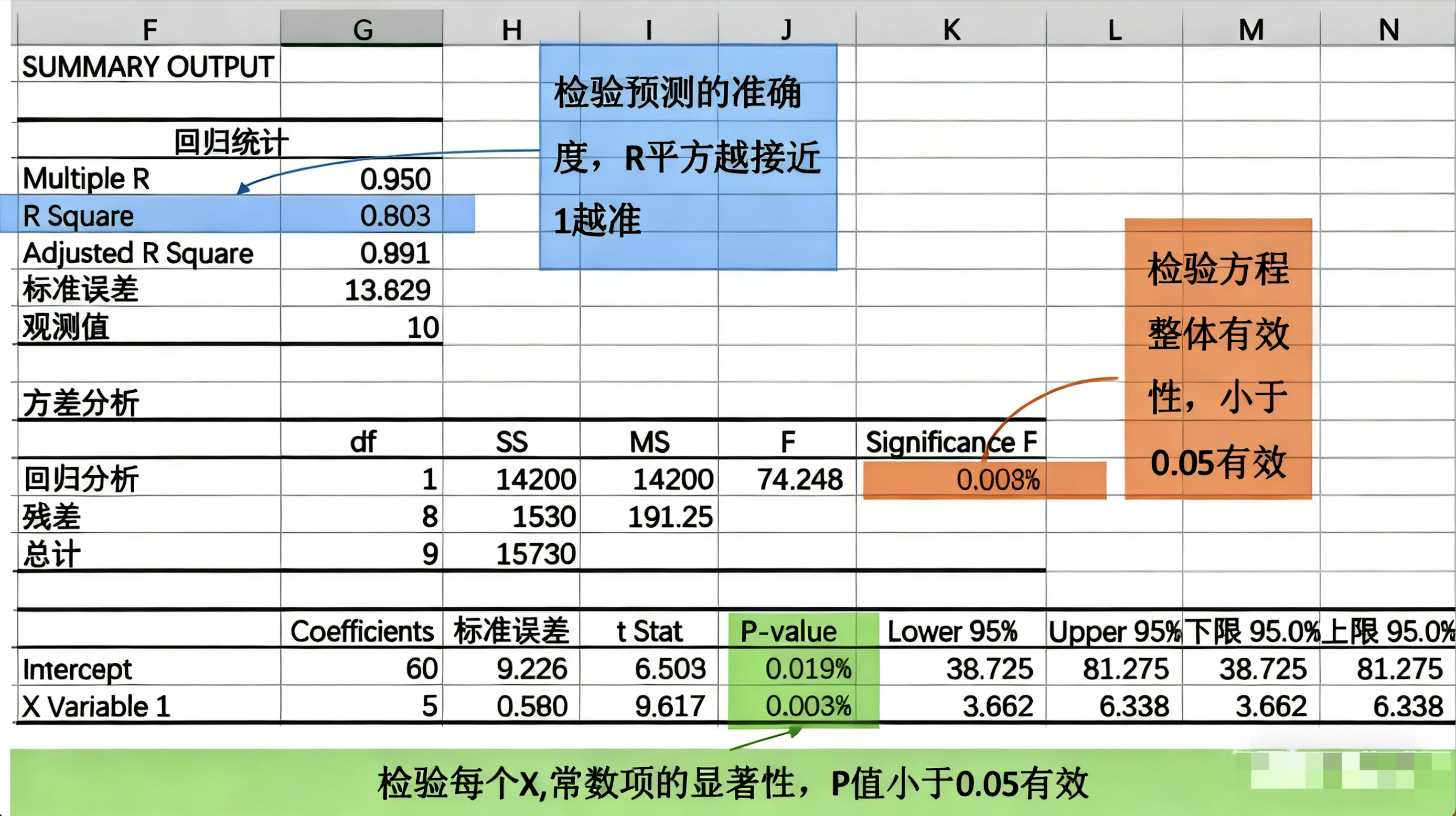
从上图可以看出,本次建模的三个检验结果全部通过,表明模型可用。
这次建模只有一个自变量 + 一个常数项,因此最终模型就是 y=60+5x。意思是:即使没人预约,也有60的基础销量;每增加1个预约用户,销量平均提升5个单位。
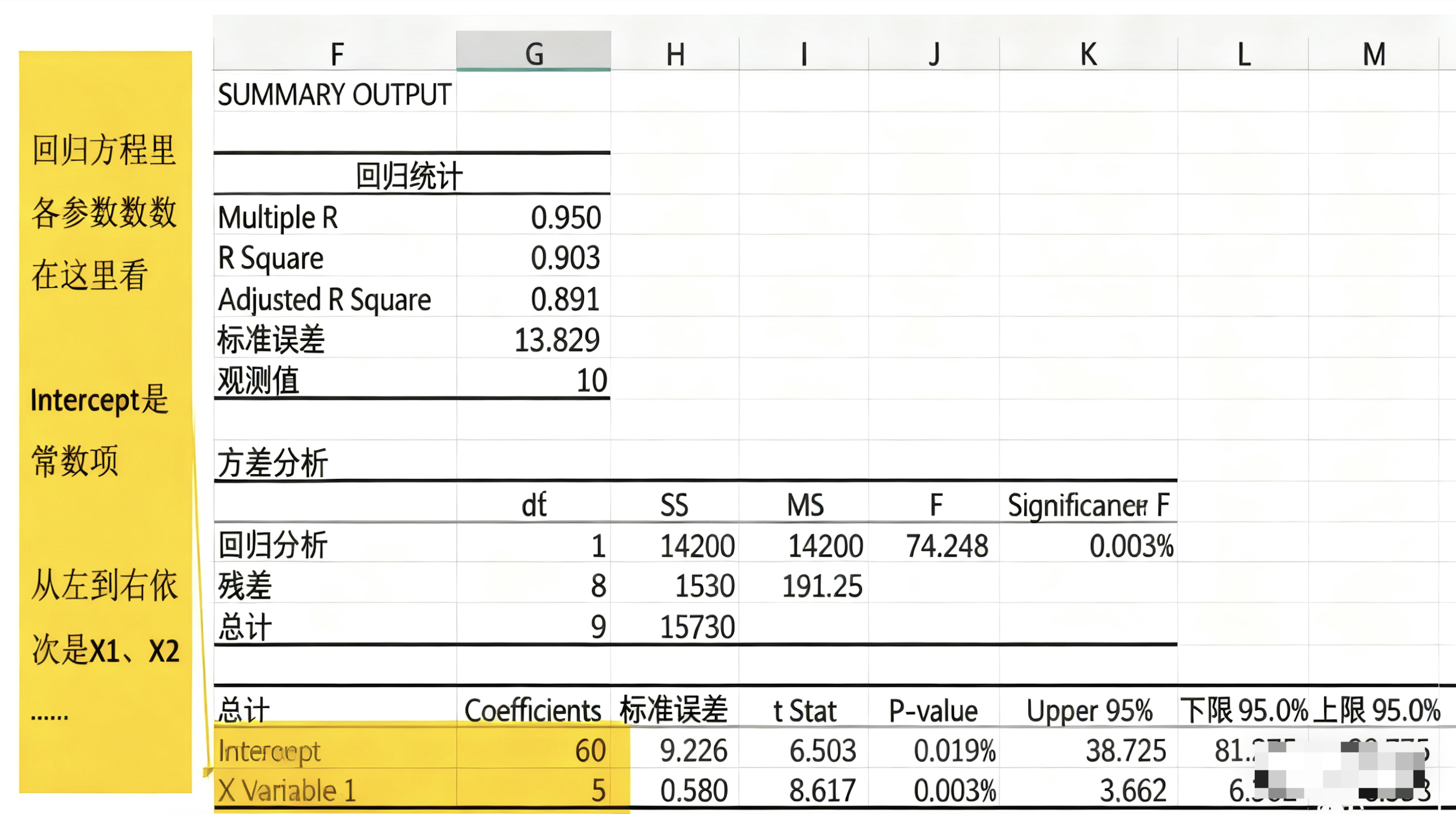
写在最后
回归模型虽然好用,但不是万能的
1、回归不等于因果!它只能说明两个变量“相关”,并不代表一个导致另一个。比如“冰淇淋销量与溺水人数正相关”,但显然不是冰淇淋害的。背后可能是“气温”这个共同因素。
2、模型检验可能难以通过。为了演示方便,例子里的数据很干净,三项检验全通过。但在真实业务中,数据往往杂乱、异常点多,可能出现各种检验不过的情况。这也是为什么后续衍生出了岭回归、LASSO 回归等更复杂的模型。
总结来说,回归分析是从数据中找到趋势、验证假设、量化影响的过程。它虽然不万能,但是却很有效,能帮你把你的认为,变成实打实的数据。

热门产品推荐