7个回归分析模型，数据分析师必看 | 帆软九数云

九数云BI小编 | 发表于：2025-09-24 16:57:56

你是否曾好奇：房价和面积、学区、房龄之间到底有什么关系？广告投入增加 10%，销量会提升多少？员工的工作年限、学历与薪资水平是否存在必然联系？这些问题的核心，都是探索变量之间的关系—— 而回归分析模型，正是解开这类问题的钥匙。

作为统计学中最经典的分析方法之一，回归分析通过建立数学模型，量化变量间的依赖关系，帮我们从杂乱的数据中找到规律、预测趋势。无论是科研实验、商业决策还是日常生活，回归分析都在默默发挥作用。

今天，本文就来聊聊7种最常用的回归分析模型，看看它们各自擅长解决什么问题，又该如何选择。

一、回归分析模型综述

虽然回归模型有很多种，但它们的核心逻辑是一致的： 找到一个因变量，和若干自变量，通过数学公式描述它们之间的关系。

比如，房价是因变量，面积、学区、房龄是自变量，回归模型会告诉你：面积每增加 1 平米，房价平均上涨多少；学区房比非学区房贵多少……

不同回归模型的区别，主要在于因变量的类型和变量间的关系形态：

如果因变量是连续的，如房价、薪资，可以用线性回归、多项式回归
如果因变量是分类的，如是否购买产品、疾病是否发生，则需要用逻辑回归
如果变量间的关系不是直线，而是曲线或分段变化，就需要用非线性回归、分段回归……

选择模型的关键，就是根据数据特点和研究目标，匹配最合适的关系形态。

二、7 个回归分析模型介绍

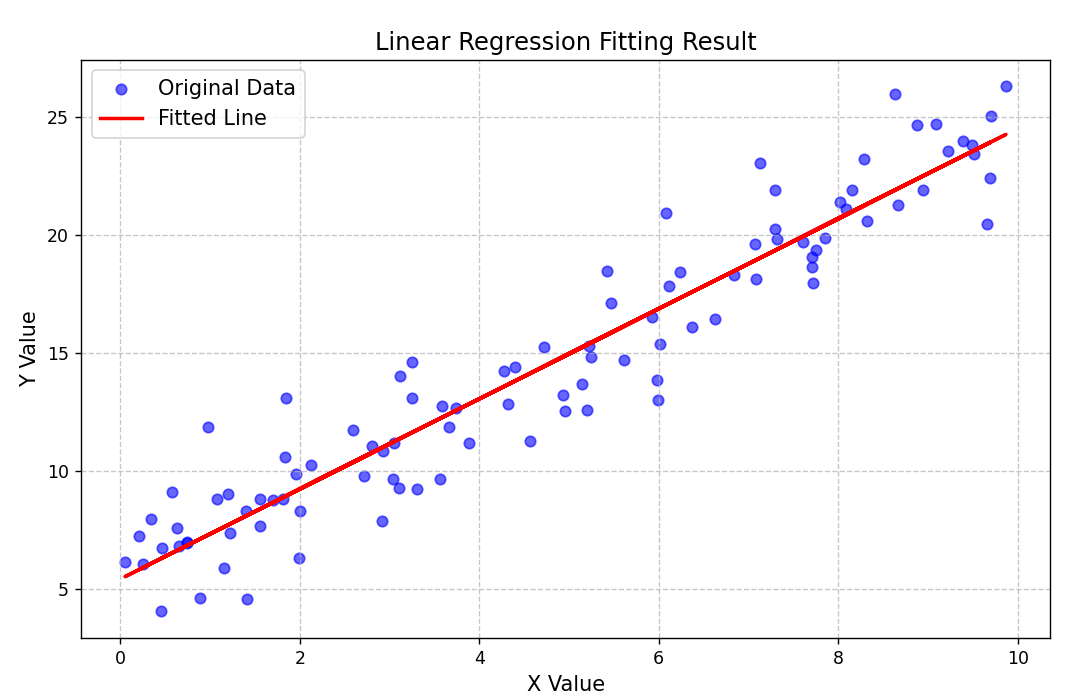
1. 线性回归

线性回归假设因变量与自变量呈线性关系，用直线描述。

适用场景：

因变量是连续变量，如收入、温度、销量
自变量与因变量的关系近似直线，可通过散点图判断

举个例子：

分析广告投入与月销量的关系，线性回归会给出公式：

销量 = 5000 + 2.5 × 广告投入

意思是：即使不投广告，基础销量是 5000；每多投 1 元广告，销量平均增加 2.5 元。

需要注意的是：线性回归对数据要求较严格，比如需要自变量之间相关性低、无多重共线性、误差服从正态分布等。

7个回归分析模型，数据分析师必看插图

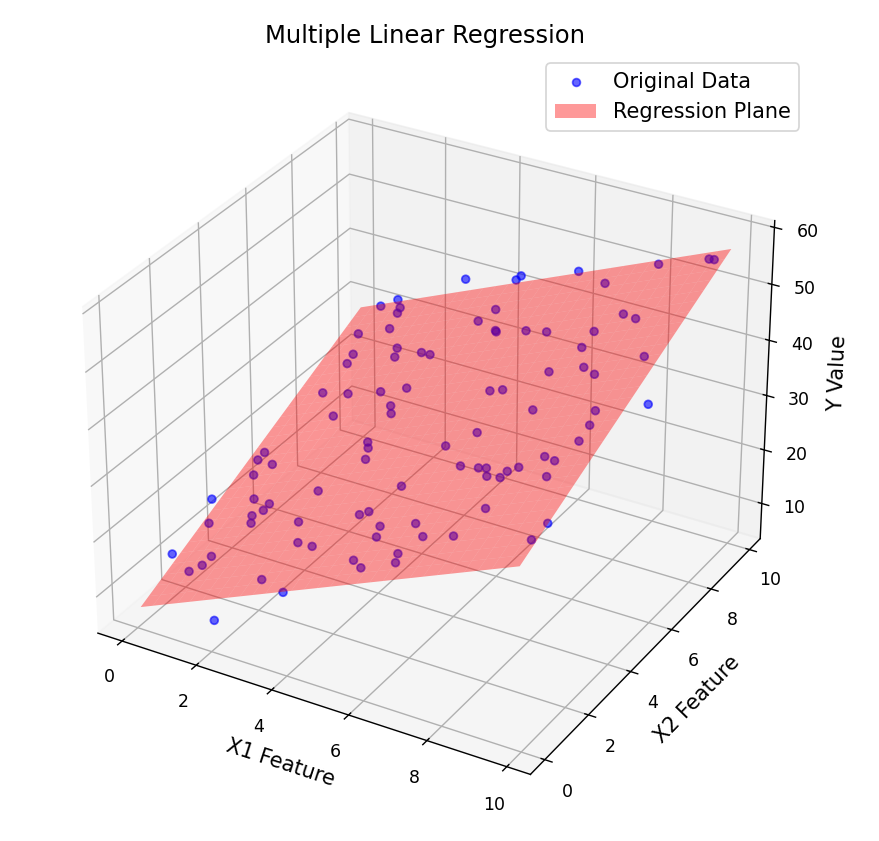
2. 多元线性回归

多元线性回归在简单线性回归的基础上，纳入多个自变量，分析它们对因变量的共同影响。

适用场景：

因变量受多个因素影响，现实中绝大多数问题都是如此
多个自变量与因变量均呈线性关系。

举个例子：

分析房价与面积、房龄、距离市中心距离的关系，模型可能为：

房价 = 100 万 + 1.2 万 × 面积 - 0.5 万 × 房龄 - 8 万 × 距离（公里）

结果说明：面积越大、房龄越小、离市中心越近，房价越高，且每个因素的影响力度不同。

7个回归分析模型，数据分析师必看插图1

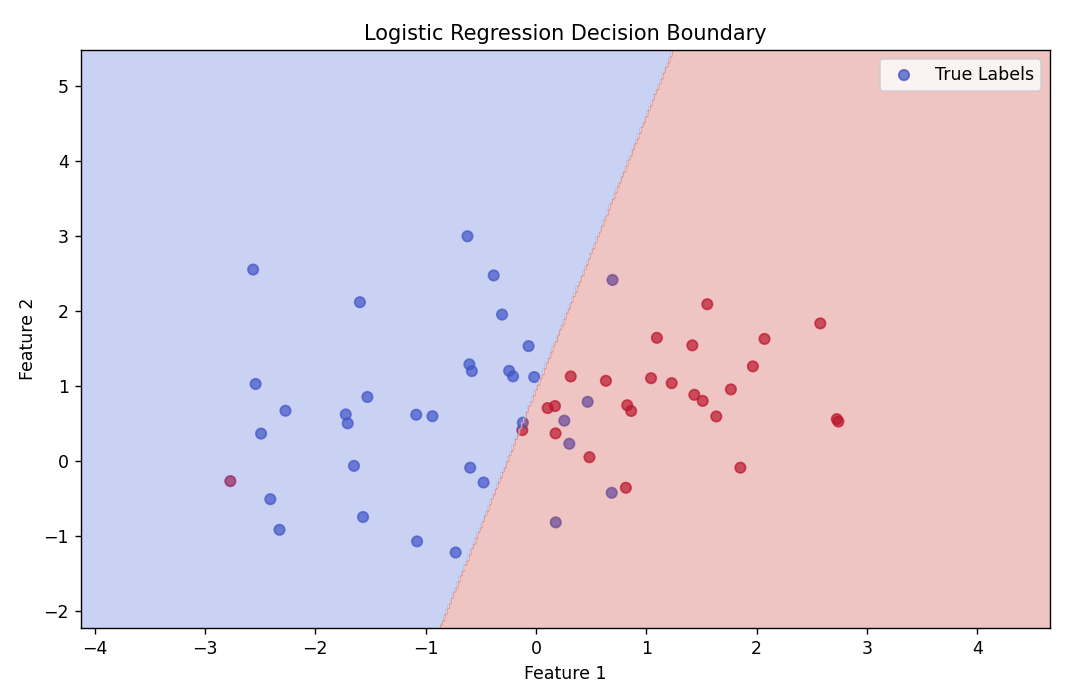
3. 逻辑回归

逻辑回归的因变量是二分类变量，如是/否、发生/不发生，通过公式将结果映射到 0-1 之间。

适用场景：

因变量是分类变量，且只有两个结果，如用户是否点击广告、患者是否患病；
想预测某事件发生的概率

举个例子：

预测用户是否购买产品，自变量包括浏览时长、历史购买次数。逻辑回归会输出：

购买概率 = 1 / [1 + e^-(0.3× 浏览时长 + 0.8× 购买次数 - 2)]

当概率＞0.5 时，预测会购买；否则不会购买

7个回归分析模型，数据分析师必看插图2

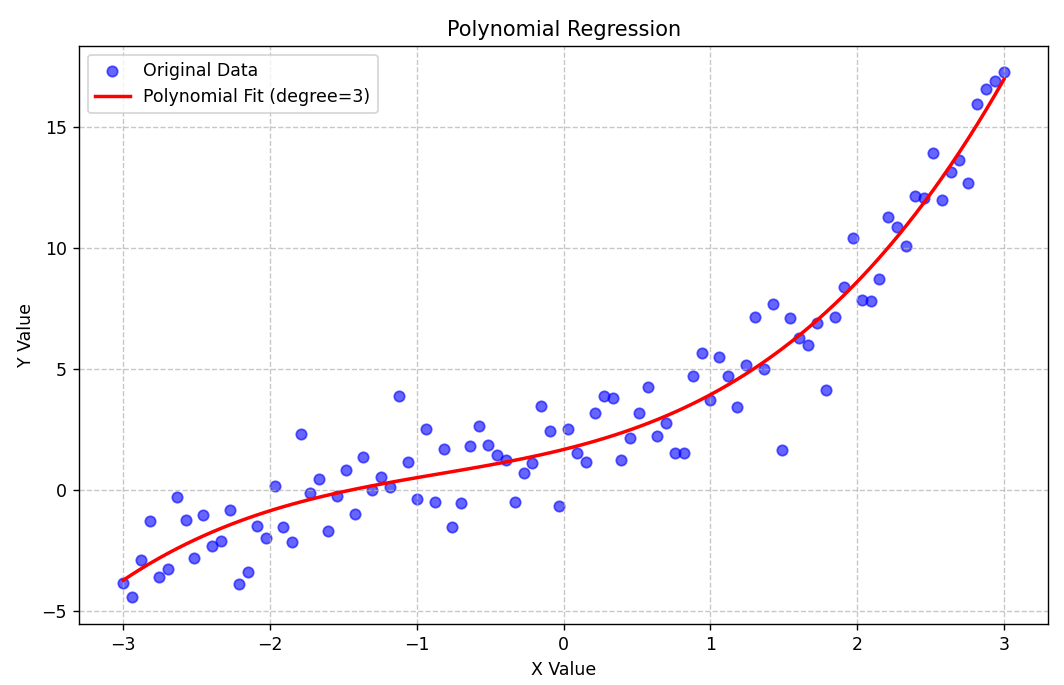
4. 多项式回归

多项式回归是当自变量与因变量的关系是曲线，如二次曲线、三次曲时，用多项式拟合。

适用场景：

变量间关系不是直线，比如年龄与收入：年轻时收入随年龄增长快，中年后增长放缓甚至下降
散点图呈现明显的曲线趋势

举个例子：

分析年龄与月收入，多项式回归可能给出：

收入 = -500× 年龄 ² + 30000× 年龄 - 200000

这个二次函数的图像是一条抛物线，能准确描述收入先增后减的趋势。

7个回归分析模型，数据分析师必看插图3

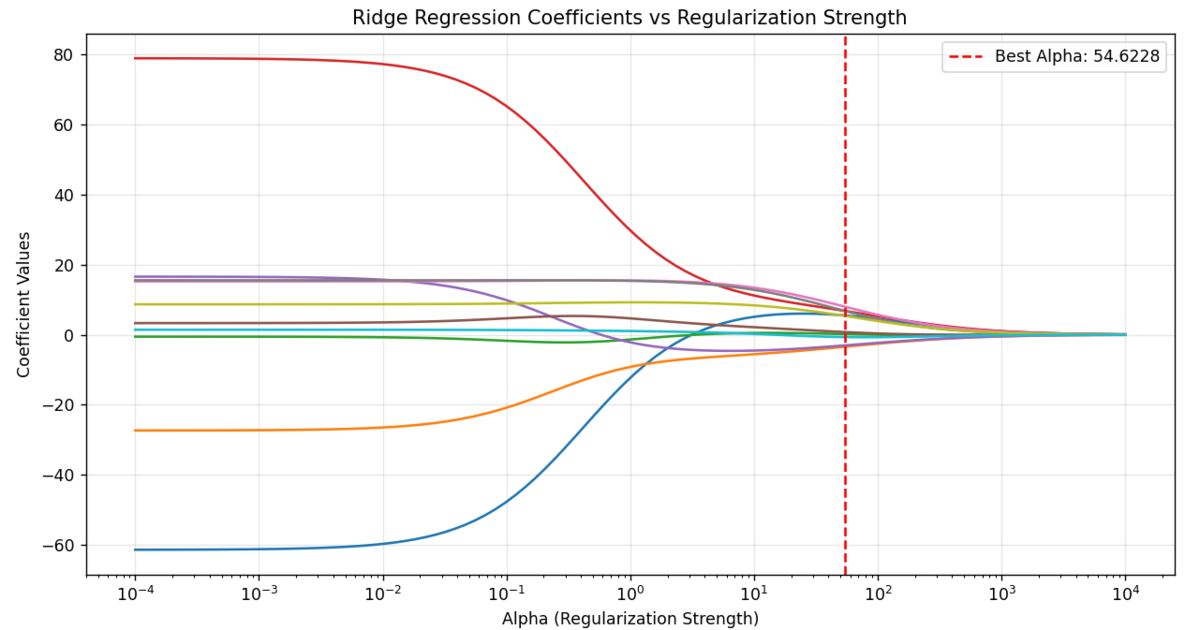
5. 岭回归

岭回归是当自变量之间高度相关时，通过正则化避免结果失真。

适用场景：

自变量数量多，且存在强相关性
线性回归结果不稳定

举个例子：

分析学生成绩与每天学习时长、每周做题量、参加辅导班次数，这三个自变量可能高度相关，学习时间长的学生，做题量和辅导班次数也可能多。

此时用岭回归，能弱化多重共线性的影响，得到更可靠的系数。

7个回归分析模型，数据分析师必看插图4

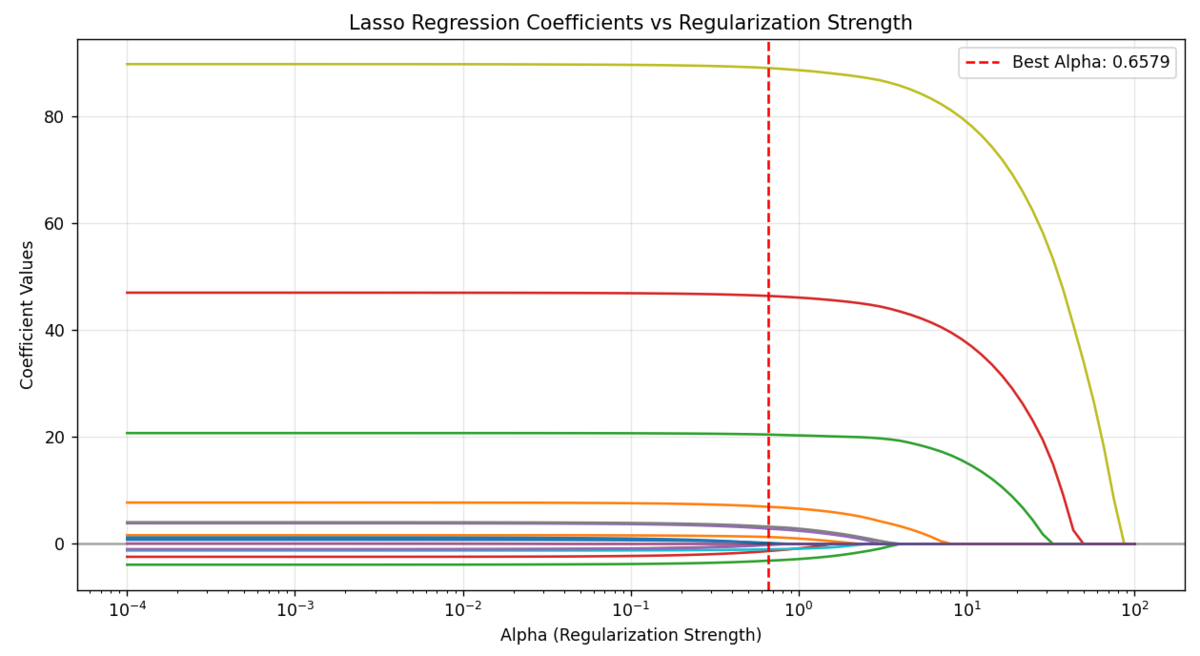
6. LASSO 回归

LASSO 回归不仅能解决多重共线性，还能通过正则化压缩部分自变量的系数为 0，自动实现变量筛选。

适用场景：

自变量数量极多，如基因数据、用户行为特征，想找出真正有影响的因素
希望模型更简洁，只保留关键变量

举个例子：

分析高血压患病风险与 100 个生活习惯变量，LASSO 回归会自动将每天喝水量、是否熬夜等无关变量的系数设为 0，只保留盐摄入量、运动频率等关键因素，让模型更易解释。

区别于岭回归：岭回归会缩小系数但不设为 0，LASSO 回归直接剔除无关变量，更适合高维数据。

7个回归分析模型，数据分析师必看插图5

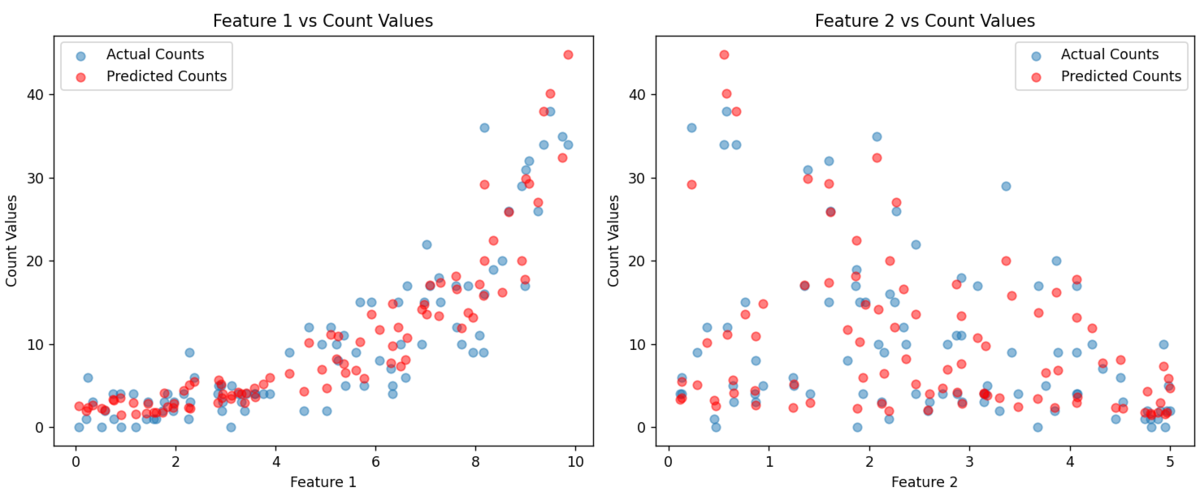
7. 泊松回归

泊松回归的因变量是计数变量，如一定时间内的发生次数，且数值是非负整数。

适用场景：

因变量是事件发生的次数，如每月交通事故数、患者每天咳嗽次数
数据呈现右偏分布

举个例子：

分析城市每月交通事故数与车流量、雨天次数、交通灯数量的关系，泊松回归会量化：

车流量每增加 1000 辆，事故数平均增加多少；雨天每多 1 天，事故数上升多少。

7个回归分析模型，数据分析师必看插图6

结束语

7 种回归分析模型，各有各的擅长：线性回归帮我们抓基础关系，逻辑回归解决分类问题，多项式回归捕捉曲线趋势，岭回归和 LASSO 回归处理复杂数据……

而在实际应用这些回归分析方法时，一款好用的工具能让分析过程更高效。九数云就是这样一款不错的工具，能帮助你更轻松地处理数据、建立模型，从而更好地从数据中挖掘价值，为决策提供有力支持。

7个回归分析模型，数据分析师必看插图7

免费注册

咨询方案

7个回归分析模型，数据分析师必看 | 帆软九数云

一、回归分析模型综述